Underdamped Diffusion Samplers Outperform Traditional Methods: Researchers from Karlsruhe Institute of Technology, NVIDIA, and Zuse Institute Berlin Introduce a New Framework for Efficient Sampling from Complex Distributions with Degenerate Noise

Diffusion processes have emerged as promising approaches for sampling from complex distributions but face significant challenges when dealing with multimodal targets. Traditional methods based on overdamped Langevin dynamics often exhibit slow convergence rates when navigating between different modes of a distribution. While underdamped Langevin dynamics have shown empirical improvements by introducing an additional momentum variable, fundamental limitations remain. The degenerate noise structure in underdamped models where Brownian motion couples indirectly to the space variable creates smoother paths but complicates theoretical analysis.

Existing methods like Annealed Importance Sampling (AIS) bridge prior and target distributions using transition kernels, while Unadjusted Langevin Annealing (ULA) implements uncorrected overdamped Langevin dynamics within this framework. Monte Carlo Diffusion (MCD) optimizes targets to minimize marginal likelihood variance, while Controlled Monte Carlo Diffusion (CMCD) and Sequential Controlled Langevin Diffusion (SCLD) focus on kernel optimization with resampling strategies. Other approaches prescribe backward transition kernels, including the Path Integral Sampler (PIS), the Time-Reversed Diffusion Sampler (DIS), and the Denoising Diffusion Sampler (DDS). Some methods, like the Diffusion Bridge Sampler (DBS), learn both forward and backward kernels independently.

Researchers from the Karlsruhe Institute of Technology, NVIDIA, Zuse Institute Berlin, dida Datenschmiede GmbH, and FZI Research Center for Information Technology have proposed a generalized framework for learning diffusion bridges that transport prior distributions to target distributions. This approach contains both existing diffusion models and underdamped versions with degenerate diffusion matrices where noise affects only specific dimensions. The framework establishes a rigorous theoretical foundation, showing that score-matching in underdamped cases is equivalent to maximizing a likelihood lower bound. This approach addresses the challenge of sampling from unnormalized densities when direct samples from the target distribution are unavailable.

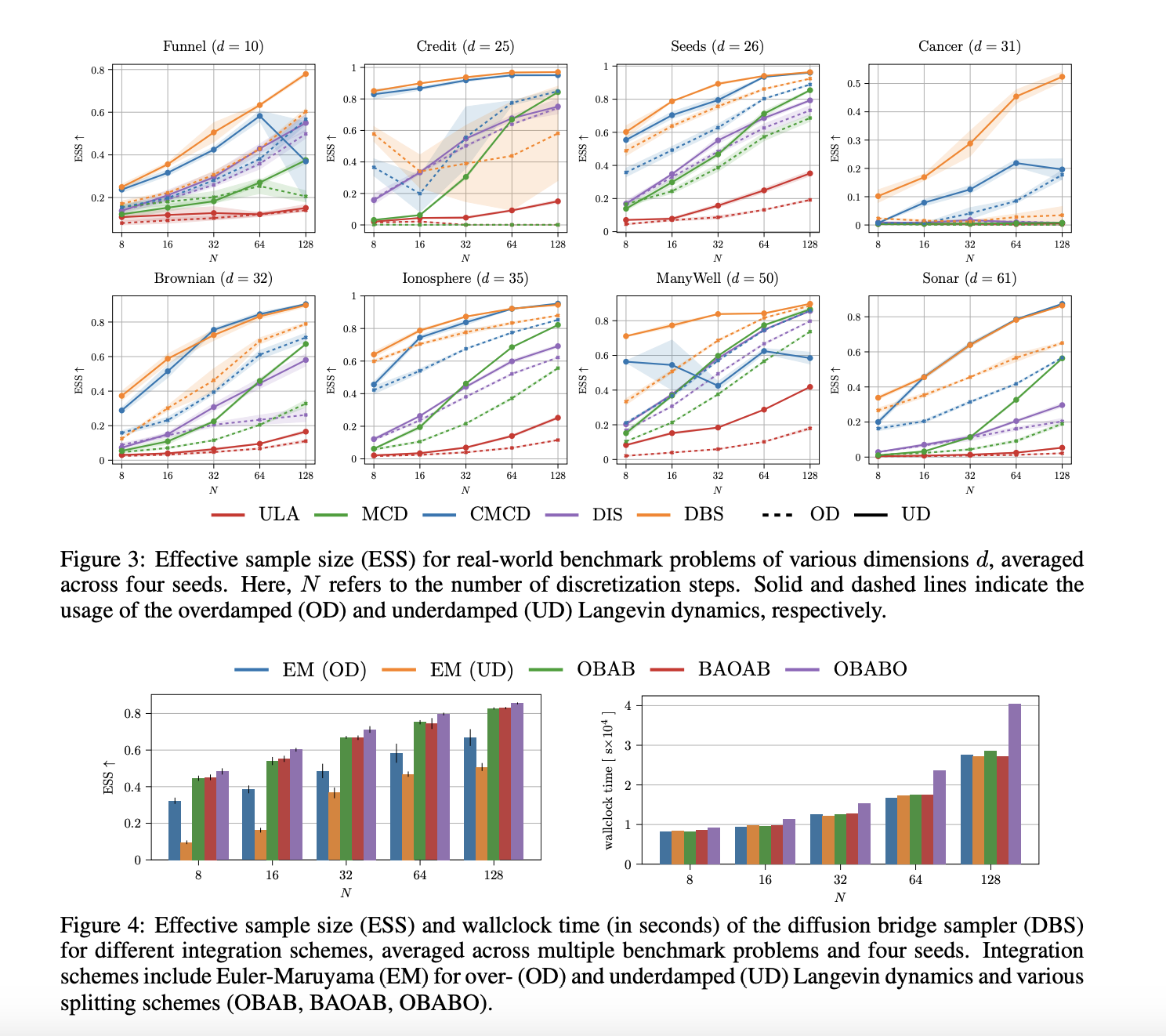
The framework enables a comparative analysis between five key diffusion-based sampling methods: ULA, MCD, CMCD, DIS, and DBS. The underdamped variants of DIS and DBS represent novel contributions to the field. The evaluation methodology uses a diverse testbed including seven real-world benchmarks covering Bayesian inference tasks (Credit, Cancer, Ionosphere, Sonar), parameter inference problems (Seeds, Brownian), and high-dimensional sampling with Log Gaussian Cox process (LGCP) having 1600 dimensions. Moreover, synthetic benchmarks include the challenging Funnel distribution characterized by regions of vastly different concentration levels, providing a rigorous test for sampling methods across varied dimensionality and complexity profiles.

The results show that underdamped Langevin dynamics consistently outperform overdamped alternatives across real-world and synthetic benchmarks. The underdamped DBS surpasses competing methods even when using as few as 8 discretization steps. This efficiency translates to significant computational savings while maintaining superior sampling quality. Regarding numerical integration schemes, specialized integrators show marked improvements over classical Euler methods for underdamped dynamics. The OBAB and BAOAB schemes deliver substantial performance gains without extra computational overhead, while the OBABO scheme achieves the best overall results despite requiring double evaluation of control parameters per discretization step.

In conclusion, this work establishes a comprehensive framework for diffusion bridges that contain degenerate stochastic processes. The underdamped diffusion bridge sampler achieves state-of-the-art results across multiple sampling tasks with minimal hyperparameter tuning and few discretization steps. Thorough ablation studies confirm that the performance improvements stem from the synergistic combination of underdamped dynamics, innovative numerical integrators, simultaneous learning of forward and backward processes, and end-to-end learned hyperparameters. Future directions include benchmarking underdamped diffusion bridges for generative modeling applications using the evidence lower bound (ELBO) derived in Lemma 2.4.

Check out Paper. All credit for this research goes to the researchers of this project. Also, feel free to follow us on Twitter and don’t forget to join our 85k+ ML SubReddit.

Sajjad Ansari is a final year undergraduate from IIT Kharagpur. As a Tech enthusiast, he delves into the practical applications of AI with a focus on understanding the impact of AI technologies and their real-world implications. He aims to articulate complex AI concepts in a clear and accessible manner.